Bài giảng Hình học Lớp 8 - Chương II: Đa giác. Diện tích đa giác - Bài 1: Đa giác. Đa giác đều

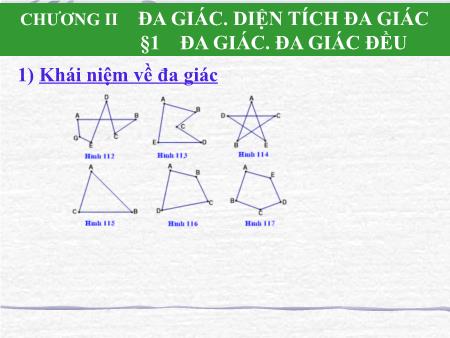
 CHƯƠNG II ĐA GIÁC. DIỆN TÍCH ĐA GIÁC 
 §1 ĐA GIÁC. ĐA GIÁC ĐỀU
1) Khái niệm về đa giác CHƯƠNG II ĐA GIÁC. DIỆN TÍCH ĐA GIÁC 
 §1 ĐA GIÁC. ĐA GIÁC ĐỀU
1) Khái niệm về đa giác.
 Đa giác ABCDE là hình gồm năm đoạn thẳng AB, BC, 
 CD, DE, EA trong đó bất kỳ hai đoạn thẳng nào có một 
 điểm chung cũng không cùng nằm trên một đường thẳng.
 ?1 Tại sao hình gồm 
 năm đoạn thẳng AB, 
 BC, CD, DE, EA ở 
 hình 118 không phải 
 là đa giác ? F
 B
 A
 G
 E H D C
Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường 
thẳng chứa bất kỳ cạnh nào của tứ giác. * Định nghĩa đa giác lồi.
 Đa giác lồi là đa giác luôn nằm trong một nửa 
 mặt phẳng có bờ là đường thẳng chứa bất kỳ 
 cạnh nào của đa giác đó. Đa giác lồi là đa giác luôn nằm trong một nửa mặt phẳng có bờ là 
 đường thẳng chứa bất kỳ cạnh nào của đa giác đó.
 ?2 Tại sao các đa giác ở hình 112, 113, 114 
 không phải là đa giác lồi ?
 Chú ý: Từ nay,khi nói đến đa giác mà không chú thích gì thêm, 
ta hiểu đó là đa giác lồi. A
 Quan sát đa giác ABCDEG ở hình 119 rồi 
 ?3 điền vào chỗ trốnga trong các câu sau:
Đa giác ABCDEG có:
- Các đỉnh là: A, B, 
- Các đỉnh kề nhau là: A và B, hoặc 
B và C, hoặc 
- Các cạnh là: AB, BC, 
- Các đường chéo là: AC, CG, 
- Các góc là: , 
- Các điểm nằm trong đa giác là: M, 
N, 
 Hình 119
- Các điểm nằm ngoài đa giác là: 
Q, Đa giác có n đỉnh (n 3) được gọi là hình n-giác hay 
hình n-cạnh.
 Với n = 3, 4, 5, 6, 8 ta quen gọi là tam giác, tứ giác, 
ngũ giác, lục giác, bát giác.
 Với n = 7, 9, 10, ta gọi là hình 7 cạnh, hình 9 cạnh, 
hình 10 cạnh, Chương II: ĐA GIÁC. DIỆN TÍCH ĐA GIÁC 
 §1 ĐA GIÁC. ĐA GIÁC ĐỀU
1) Khái niệm về đa giác
 * Khái niệm đa giác.
 * Định nghĩa đa giác lồi.
 2) Đa giác đều
 Em hãy cho biết độ 
 dài các cạnh và số đo 
 các góc trong các hình 
 vẽ sau. Chương II: ĐA GIÁC. DIỆN TÍCH ĐA GIÁC 
 §1 ĐA GIÁC. ĐA GIÁC ĐỀU
1) Khái niệm về đa giác
 * Khái niệm đa giác.
 * Định nghĩa đa giác lồi.
2) Đa giác đều
 Đa giác đều là đa giác có tất cả các cạnh bằng 
nhau và tất cả các góc bằng nhau.
 Hình thoi và chữ nhật có phải là đa giác đều không ? Vì sao ? Hãy vẽ các trục đối xứng và tâm đối xứng (nếu 
?4 có) của các hình sau: Điền số thích hợp vào các ô trống trong bảng sau:
 Đa giác 
 n cạnh
Số cạnh 4 5 6 n
Số đường chéo 
xuất phát từ một 1 2 3 n - 3
đỉnh
Số tam giác được 2 3 n - 2
tạo thành 4
 0 0 4.1800 
Tổng số đo các 2.180 3.180 (n-2).1800
góc của đa giác = 3600 = 5400 = 7200 * Học thuộc và nắm chắc khái niệm đa giác, định nghĩa đa 
giác lồi; đa giác đều. Công thức tính tổng các góc của đa giác.
* Làm các bài tập: 1, 3 – SGK. Bài 2, 3, 5 - SBT.
* Xem trước bài: “Diện tích hình chữ nhật”
* Ôn tập công thức tính diện tích: tam giác, hình chữ nhật, 
hình vuông.
* Chuẩn bị thước thẳng, êke, kéo, cắt các hình A, B, C, D như 
hình 121 trang 116 - SGK. Bài 3 Cho hình thoi ABCD có góc A bằng 600. 
 A§SSSD
Gọi E, F, G, H lần lượt là trung điểm của các cạnh 
AB, BC, CD, DA. Chứng minh rằng đa giác 
EBFGDH là lục giác đều. Cách vẽ lục giác đều
 B C
 B C
 A O r D D
A O
 F E
 F E