Bài giảng Hình học Lớp 8 - Chương II: Đa giác. Diện tích đa giác - Bài 5: Diện tích hình thoi

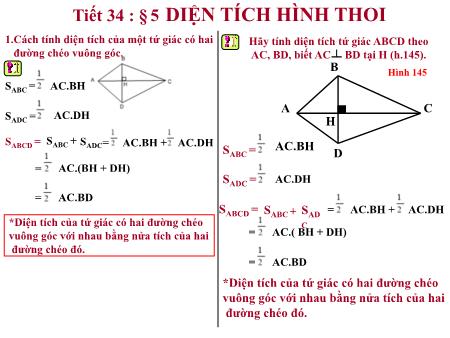
 Tiết 34 : § 5 DIỆN TÍCH HÌNH THOI
1.Cách tính diện tích của một tứ giác có hai Hãy tính diện tích tứ giác ABCD theo
 đường chéo vuông góc. AC, BD, biết AC BD tại H (h.145).
 B Hình 145
SABC = AC.BH
 A C
S = AC.DH
 ADC H
 S +
SABCD = ABC SADC= AC.BH + AC.DH AC.BH
 SABC = D
 = AC.(BH + DH) 
 SADC = AC.DH
 = AC.BD 
 SABCD = SABC + SAD = AC.BH + AC.DH 
 *Diện tích của tứ giác có hai đường chéo C
 vuông góc với nhau bằng nửa tích của hai = AC.( BH + DH) 
 đường chéo đó.
 = AC.BD
 *Diện tích của tứ giác có hai đường chéo 
 vuông góc với nhau bằng nửa tích của hai
 đường chéo đó. Tiết 34 : § 5 DIỆN TÍCH HÌNH THOI
1.Cách tính diện tích của một tứ giác có Hãy viết công thức tính diện tích hình 
 hai đường chéo vuông góc. thoi theo hai đường chéo.
 *Diện tích của tứ giác có hai đường chéo 
 vuông góc với nhau bằng nửa tích của hai
 đường chéo đó. d2
2.Công thức tính diện tích hình thoi
 d1
S = d .d d2
 1 2 *Diện 3 Hãy tích tính hình diện thoitích hình bằng thoi nửa bằng tích 
 cách khác.
 hai đườngchéo.S = d1.d2
 d1 Hình thoi cũng như hình bình hành.
•Diện tích hình thoi bằng nửa tích
 hai đườngchéo. S = a.h
 a
 h
 a
 S = a.h h Tiết 34 : § 5 DIỆN TÍCH HÌNH THOI
1.Cách tính diện tích của một tứ giác có Ví dụ
 hai đường chéo vuông góc. Trong một khu vườn hình thang cân ABCD 
 ( đáy nhỏ AB = 30 m, đáy lớn CD = 50 m, diện 
 tích bằng 800 ), người ta làm một bồn hoa
 *Diện tích của tứ giác có hai đường chéo 
 hình tứ giác MENG với M, E, N, G là trung 
 vuông góc với nhau bằng nửa tích của hai
 điểm các cạnh của hình thang cân. (h.146)
 đường chéo đó.
 a) Tứ giác MENG là hình gì?
2.Công thức tính diện tích hình thoi
 b) Tính diện tích của bồn hoa. H.146
 20m
 d
 2 A E B
 S = d1.d2
 d
 1 M N
*Diện tích hình thoi bằng nửa tích hai đường Nhắc lạiABCD tính chất là đườnghình thang trung cân,bình của
chéo. tam giác?AB=30m, CD=50m, 
 GT
 2
 SABCD=800m
3. Ví dụ DĐườngTứ trung giác bình MENG củaG làtam hình giác gì? thì song C
 songKL với cạnh= thứ ? ba50m và bằng nửa cạnh ấy.
 SMENG 
 2
 a) STứABCD giác = 800m MENG là hình gì?
 b) Tính diện tích của bồn hoa. Tiết 34 : § 5 DIỆN TÍCH HÌNH THOI
1.Cách tính diện tích của một tứ giác có Ví dụ a) Tứ giác MENG là hình gì?
 hai đường chéo vuông góc. b) Tính diện tích của bồn hoa.
 A E 30m B H.146
 *Diện tích của tứ giác có hai đường chéo 
 vuông góc với nhau bằng nửa tích của hai
 đường chéo đó. M N
2.Công thức tính diện tích hình thoi
 d
 2 D G C
 S = d1.d2 2 50m
 SABCD = 800m
 d1 Giải
*Diện tích hình thoi bằng nửa tích hai đường
chéo. a) ME // BD và ME = BD
3. Ví dụ a) ME // BD và ME = BD GN // BD và GN = BD
 => ME // GN và ME = GN
 GN // BD và GN = BD => MENG là hình bình hành 
 => ME // GN và ME = GN
 => MENG là hình bình hành Tương tự, ta có EN//AC và EN = AC
 Tương tự, ta có EN//AC và EN = AC Mặt khác ta có AC = BD, suy ra ME =EN 
 Vậy MENG là hình thoi 
 Mặt khác ta có AC = BD, suy ra ME =EN 
 Vậy MENG là hình thoi Tiết 34 : § 5 DIỆN TÍCH HÌNH THOI
1.Cách tính diện tích của một tứ giác có Ví dụ a) Tứ giác MENG là hình gì?
 hai đường chéo vuông góc. b) Tính diện tích của bồn hoa.
 30m H.146
 *Diện tích của tứ giác có hai đường chéo A E B
 vuông góc với nhau bằng nửa tích của hai
 đường chéo đó.
2.Công thức tính diện tích hình thoi M N
 d2 D C
 S = d1.d2 G
 d1 S = 800m2
*Diện tích hình thoi bằng nửa tích hai đường ABCD 50m
chéo. Giải
 b)Để MN tính là diện đường tích thẳng hình trungthoi MENG bình của ta cầnhình 
3. Ví dụ a) ME // BD và ME = BD thangbiết gì? nên MN và EG 
 MN= 
 GN // BD và GN = BD
 => ME // GN và ME = GN EG là đường cao của hình thang ABCD
 => MENG là hình bình hành Nên MN.EG = 800 => EG = 800 : 40 = 20(m)
 Tương tự, ta có EN//AC và EN = AC
 S = MN.EG = 40.20 = 400 (m2)
 Mặt khác ta có AC = BD, suy ra ME =EN MENG
 Vậy MENG là hình thoi Tiết 34 : § 5 DIỆN TÍCH HÌNH THOI
1.Cách tính diện tích của một tứ giác có A
 Bài tập 46:
 hai đường chéo vuông góc.
 D O B 12cm
 *Diện tích của tứ giác có hai đường chéo H
 vuông góc với nhau bằng nửa tích của hai C
 16cm
 đường chéo đó. Tính: a) Diện tích hình thoi.
2.Công thức tính diện tích hình thoi b) Độ dài cạnh hình thoi.
 c) Độ dài đường cao hình thoi.
 d GIẢI
 2 a, Diện tích hình thoi:
 S = d1.d2
 2
 SABCD = 16.12 = 96 (cm )
 d1
*Diện tích hình thoi bằng nửa tích hai đường
 b) Trong tam giác vuông AOB ta có:
chéo.
 AB=
3. Ví dụ c) Gỉa sử AH là đường cao hình thoi kẻ từ 
*Bài tập củng cố đỉnh A, ta có 
 Bài tập 46 SABCD = AH.CD
 Do đó : AH = Tiết 34 : § 5 DIỆN TÍCH HÌNH THOI
1.Cách tính diện tích của một tứ
 BÀI TẬP VỀ NHÀ 
 giác có hai đường chéo vuông góc.
 • Học thuộc bài
*Diện tích của tứ giác có hai đường • Thực hiện bài tập 35, 36 (SGK)
chéo vuông góc với nhau bằng nửa tích • Chuẩn bị bài trước để tiết sau 
 của hai đường chéo đó. luyện tập.
2.Công thức tính diện tích hình thoi
 d
 S = d1.d2 2
 d1
*Diện tích hình thoi bằng nửa tích hai 
Đường chéo.
3. Ví dụ