Đề luyện thi đánh giá năng lực các môn Lớp 12 năm 2022 - Đề số 4 (Có đáp án)

 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
 EMPIRE TEAM 
 ĐỀ SỐ 4 
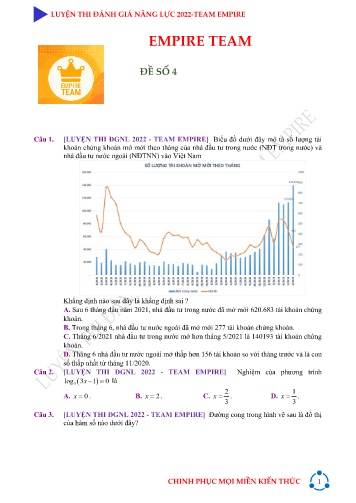
Câu 1. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Biểu đồ dưới đây mô tả số lượng tài 
 khoản chứng khoán mở mới theo tháng của nhà đầu tư trong nước (NĐT trong nước) và 
 nhà đầu tư nước ngoài (NĐTNN) vào Việt Nam 
 Khẳng định nào sau đây là khẳng định sai ? 
 A. Sau 6 tháng đầu năm 2021, nhà đầu tư trong nước đã mở mới 620.683 tài khoản chứng 
 khoán. 
 B. Trong tháng 6, nhà đầu tư nước ngoài đã mở mới 277 tài khoản chứng khoán. 
 C. Tháng 6/2021 nhà đầu tư trong nước mở hơn tháng 5/2021 là 140193 tài khoản chứng 
 khoán. 
 D. Tháng 6 nhà đầu tư nước ngoài mở thấp hơn 156 tài khoản so với tháng trước và là con 
 số thấp nhất từ tháng 11/2020. 
Câu 2. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Nghiệm của phương trình 
 log3 ( 3x −= 1) 0 là 
 2 1
 A. x = 0 . B. x = 2 . C. x = . D. x = . 
 3 3
Câu 3. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Đường cong trong hình vẽ sau là đồ thị 
 của hàm số nào dưới đây? 
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 1 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 A. yx=−−3 21 x . B. yx=−−+3 21 x. C. y=−++ xx321. D. 
 yx=−+3 21 x . 
 x +1
Câu 4. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Tiệm cận ngang của đồ thị hàm số y = là 
 x −1
 A. y = 2 . B. y = 0. C. y =1. D. y = −1. 
Câu 5. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình nón có bán kính đáy r = 3 
 và độ dài đường sinh l = 4. Diện tích xung quanh của hình nón đã cho là 
 A. Sxq = 39π . B. Sxq =12π . C. Sxq = 83π . D. Sxq = 43π . 
Câu 6. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số fx( ) có đạo hàm trên . 
 fx( )
 Biết Fx( ) = sin x là một nguyên hàm của trên khoảng (0; +∞), họ tất cả các nguyên 
 x
 hàm của hàm số gx( ) = f′( x)ln x là 
 A. xln x sin x++ cos xC. B. xln x sin x−+ cos xC. 
 C. xln x cos x++ sin xC. D. xln x cos x−+ sin xC. 
 2
Câu 7. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Bất phương trình 4.2xx−< 2 0 có 
 nghiệm là 
 A. x ∈( −∞;2) . B. x ∈( −∞; − 1) ∪( 2; +∞) . 
 C. x ∈( −1; +∞) . D. x ∈−( 1; 2) . 
Câu 8. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trong không gian với hệ tọa độ Oxyz , 
 mặt phẳng (P) đi qua M (−−1;3; 2) nhận véctơ n =(3;4; − 2) làm véctơ pháp tuyến. Mặt 
 phẳng (P) có phương trình là: 
 A. 3xyz+ 4 −−= 2 13 0 . B. 3xyz+ 4 −+= 2 19 0 . 
 C. −+xyz3 − 2 + 40 = . D. −+3xyz 4 − 2 −= 13 0 . 
Câu 9. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho các số thực ab,0≠ thoả mãn 
 a
 34ab= . Giá trị của bằng 
 b
 A. log4 3 . B. ln12. C. ln 0,75 . D. log3 4 . 
Câu 10. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trên mặt phẳng tọa độ Oxy , tập hợp tất 
 cả điểm biểu diễn của số phức z thỏa mãn 35+−i zi = là đường tròn có phương trình 
 22 22
 A. ( xy−1) ++( 35) =. B. ( xy+1) +−( 3) = 25 . 
 22 22
 C. ( xy−1) ++( 3) = 25 . D. ( xy+1) +−( 35) =. 
 2 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
Câu 11. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Tìm giá trị nhỏ nhất của hàm số 
 fx()= x2 − 3 x −− 4 xtrên đoạn [−2;6] 
 A. 1. B. 4. C. 0 . D. 5 . 
Câu 12. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Có bao nhiêu giá trị nguyên của tham số
 x −1
 m∈−[ 10;10] sao cho đồ thị hàm số y = có hai đường tiệm cận đứng? 
 26x2 + xm −− 3
 A. 19. B. 15. C. 17 . D. 18. 
Câu 13. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trong không gian Oxyz, cho mặt cầu 
 (S ) nhận AB là đường kính biết tọa độ A(3; 2;1) ; B(−1; 4; 3 ) . Phương trình mặt cầu (S ) 
 là 
 222 222
 A. ( xyz+1) ++( 3) ++( 2) = 24. B. ( xyz+1) ++( 3) ++( 2) = 6. 
 222 222
 C. ( xyz−1) +−( 3) +−( 2) = 24. D. ( xyz−1) +−( 3) +−( 2) = 6. 
 2 3
Câu 14. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Nếu ∫ ft( )d4 t= − và ∫ fu( )d5 u= thì 
 1 2
 3
 ∫ fx( )d x bằng: 
 1
 A. −9 . B. −1. C. 1. D. 9. 
Câu 15. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Hàm số nào dưới đây đồng biến trên tập 
 xác định của nó. 
 x x x
 e 1 x 1
 A. y = . B. y = . C. y = ( π ) . D. y = . 
 π π e
Câu 16. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Họ tất cả các nguyên hàm của hàm số 
 fx( ) =2 x + sin x là 
 2 2
 A. x++cos xC. B. x−+cos xC. 
 2 ++ 2 −+
 C. 2x cos xC. D. 2x cos xC. 
Câu 17. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình trụ biết rằng khi cắt hình trụ đã 
 cho bởi một mặt phẳng qua trục, thiết diện thu được là một hình vuông và có diện tích bằng 
 32. Diện tích xung quanh của hình trụ đã cho bằng: 
 A. 16π . B. 32π . C. 64π . D. 48π . 
Câu 18. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho đa giác đều có 2022 đỉnh. Số hình 
 chữ nhật có 4 đỉnh là 4 trong số 2022 điểm là đỉnh của đa giác đã cho là 
 4 4 2 2
 A. C2022 . B. C1011 . C. C2021 . D. C1011 . 
Câu 19. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Bác An xây bể hình trụ có thể tích 150m3
 . Đáy bể làm bằng bê tông giá 100000 đồng /m2 . Phần thân làm bằng tôn giá 90000 đồng
 /m2 , nắp bằng nhôm giá 120000 đồng /m2 . Hỏi để chi phí sản xuất bể đạt mức thấp nhất 
 thì tỷ số giữa chiều cao bể và bán kính đáy là bao nhiêu? 
 22 9 31 22
 A. . B. . C. . D. . 
 9 22 22 31
Câu 20. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Nghiệm của phương trình log4 (x −= 1) 2 
 là 
 9 7
 A. x = 3. B. x =17 . C. x = . D. x = . 
 2 2
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 3 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
Câu 21. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Một hộp bóng bàn có dạng hình hộp chữ 
 nhật. Biết rằng hộp chứa vừa khít ba quả bóng bàn được xếp theo chiều dọc, các quả bóng 
 bàn có kích thước như nhau. 
 Phần không gian còn trống trong hộp chiếm tỉ lệ 
 A. 47,% 64 . B. 65,% 09 . C. 82,% 55 . D. 83,3% . 
 2*
Câu 22. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho dãy số (un ) , biết unn =+∈1, n 
 . Số 7922 là số hạng bao nhiêu trong dãy? 
 A. 79 . B. 69 . C. 89 . D. 99 
Câu 23. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trong không gian với hệ tọa độ Oxyz , 
 cho ba điểm M (3;0;0) , N (0;− 2;0) và P(0;0; 2) . Mặt phẳng (MNP) có phương trình là 
 xyz xyz xy z xyz
 A. + +=−1. B. + +=0 . C. ++ =1. D. + +=1
 3− 22 3− 22 32− 2 3− 22
 . 
Câu 24. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình trụ có bán kính đáy r , gọi O
 và O ' là tâm của hai đường tròn đáy với OO′ = 2 r . 
 Một mặt cầu tiếp xúc với hai đáy của hình trụ tại O và O ' . Gọi VC và VT lần lượt là thể 
 VC
 tích của khối cầu và khối trụ. Khi đó bằng 
 VT
 3 3 1 2
 A. . B. . C. . D. . 
 5 4 2 3
Câu 25. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trong không gian Oxyz, cho điểm 
 xy−−12 z
 A(2;2;1) và đường thẳng d : = = ; 
 1 21 2
 xyz−−32
 d : = = . Phương trình đường thẳng d đi qua A, vuông góc với d và cắt d 
 2 1 23 1 2
 là 
 xyz−−−2 21 x−−12 yz
 A. d : = = . B. d : = = . 
 1−− 35 23− 4
 xt=2 +
  xyz−−−2 21
 C. dy:2 =( t ∈ ) . D. d : = = . 
  −−12 3
  zt=1 −
 xy+=4
Câu 26. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hệ phương trình  22 2. 
 xym+=
 Khẳng định nào sau đây là đúng? 
 A. Hệ phương trình luôn vô nghiệm. 
 B. Hệ phương trình có nghiệm với mọi m . 
 C. Hệ phương trình có nghiệm ⇔≥m 8 . 
 D. Hệ phương trình có nghiệm duy nhất ⇔≥m 2. 
 4 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
Câu 27. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Theo hình thức lãi kép, một người vay 
 ngân hàng số tiền 500 triệu đồng, lãi suất theo kì hạn 1 tháng là 1%. Người này trả nợ đều 
 đặn cho ngân hàng mỗi tháng cùng một số tiền là 10 triệu đồng. Hỏi sau ít nhất bao nhiêu 
 tháng thì người này trả hết nợ bao gồm cả gốc lẫn lãi? 
 A. 68 (tháng). B. 72 (tháng). C. 69 (tháng). D. 70 (tháng). 
Câu 28. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số y= fx() xác định và liên 
 tục trên []−1; 5 có đồ thị của hàm số y= fx′() được cho như hình vẽ. Hàm số 
 gx() = f() x2 −−21 x đồng biến trên khoảng nào dưới đây? 
 A. ()−∞;1 . B. ()1;+∞ . C. ()0; 2 . D. ()−1; 0 . 
Câu 29. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số y=+() m23 x32 + x +− mx 5
 , m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã 
 cho có hoành độ là các số dương. 
 m <−3
 A. −<32m < . B.  . C. −32 <m <− . D. m∈∅ 
 m >−2
Câu 30. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình vuông ABCD có cạnh bằng a 
 và có diện tích S1 . Nối 4 trung điểm ABCD111,,, 1 theo thứ tự của 4 cạnh AB,,, BC CD DA 
 ta được hình vuông thứ hai có diện tích S2 . Tiếp tục làm như thế, ta được hình vuông thứ 
 ba là ABCD222 2 có diện tích S3 , , và cứ tiếp tục làm như vậy mãi mãi, ta được các hình 
 vuông lần lượt có diện tích SS45, ,..., Sn ,.... Khi đó, tổng diện tích S của tất cả các hình 
 vuông đó là: 
 3
 A. Sa= 2 2 . B. Sa= 2 2 . C. Sa= 3 2 . D. Sa= 2 . 
 2
 x
Câu 31. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho các hàm số ya= , 
 y=logbc xy , = log x có đồ thị như hình vẽ. 
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 5 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 Chọn khẳng định đúng? 
 A. cba>>. B. bac>>. C. abc>>. D. bca>>. 
Câu 32. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số fx() liên tục trên khoảng 
 3
 ()0; +∞ . Biết f ()11= và xf′()()21 x−− f 21 x −= x3 , ∀x ∈()0; +∞ . Giá trị ∫ fxx()d 
 1
 bằng 
 31 21 94
 A. . B. . C. 12. D. . 
 3 4 3
Câu 33. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hai số phức zz12, thỏa mãn điều 
 22
 zz12
 kiện z1= z 2 =−= zz 121. Tính giá trị của biểu thức P = + . 
 zz21
 A. Pi=1. + B. Pi=−−1. C. Pi=1. − D. P = −1. 
Câu 34. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Người ta dựng trên mặt đất bằng phẳng 
 một chiếc lều bằng bạt từ một tấm bạt hình chữ nhật có chiều dài là 12m và chiều rộng là 
 6m bằng cách: Gập đôi tấm bạt lại theo đoạn nối trung điểm hai cạnh là chiều rộng của tấm 
 bạt sao cho hai mép chiều dài còn lại của tấm bạt sát đất và cách nhau x m (xem hình vẽ). 
 A
 C
 B
 Tìm x để khoảng không gian phía trong lều là lớn nhất? 
 x 4 x 3 x 32 x 33
 A. . B. . C. . D. . 
Câu 35. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho các số phức zzz12,, thỏa mãn 
 z1= z 2 =2, zz 12 −= 2 2 . Giá trị nhỏ nhất của biểu thức 
 P= z +− zz12 +− zz là 
 A. P =22 + 2 B. P =22 + 3. C. P =23 + . D. P =43 + . 
 ĐIỀN KHUYẾT 
Câu 36. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Tính số cạnh của một hình mười hai mặt 
 đều. 
 Đáp số: 
 Lời giải 
 Hình mười hai mặt đều có 30 cạnh. 
Câu 37. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số y= fx()có bảng biến thiên 
 như hình bên. 
 6 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
 Số nghiệm thực của phương trình 2fx ()−= 1 0là 
 Đáp số: 
Câu 38. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số y= fx( ) thỏa mãn 
 π π
 2 2
 ∫ cosxf .( x)d x= 2 , biết I= ∫ sin xf .′( x)d x= 1. Tính giá trị f (0) . 
 0 0
 Đáp số: 
Câu 39. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Một khối trụ có thể tích là 20 . Nếu tăng 
 bán kính của khối trụ nên gấp 2 lần thì thể tích khối trụ là bao nhiêu? 
 Đáp số: 
Câu 40. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Có bao nhiêu giá trị thực của tham số m 
 11
 để hàm số yx=3 −(23 m +) xmm22 +( +− 34) x đạt cực tiểu tại x =1. 
 32
 Đáp số: 
Câu 41. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Lớp 11A1 có 25 học sinh nam và 20 học 
 sinh nữ. Hỏi có bao nhiêu cách chọn ngẫu nhiên một bạn trong lớp làm lớp trưởng? 
 Đáp số: 
Câu 42. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Một viên đá có hình dạng là khối chóp 
 tứ giác đều với tất cả các cạnh bằng a . Người ta cắt khối đá đó bởi mặt phẳng song song 
 với đáy của khối chóp để chia khối đá thành hai phần có thể tích bằng nhau. Giả thiết rằng 
 tổng thể tích của hai khối đá sau vẫn bằng thể tích của khối đá ban đầu.Diện tích của thiết 
 a2
 diện khối đá bị cắt bởi mặt phẳng trên là SMNPQ = . Tính m . 
 3 m
 S
 M Q
 N H
 P
 A
 D
 O
 B C
 Đáp số: 
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 7 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 1
Câu 43. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho dãy số (u ) với u = với 
 n n nn(+ 1)
 * Su11=
 mọi n∈ và dãy số (Sn ) xác định như sau:  . 
 Snn=+≥ S−1 un n,2
 x x
 Giá trị của S = , với xy;,∈ là phân số tối giản. Tính yx− 
 100 y y
 Đáp số: 
Câu 44. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình chóp đều S. ABCD có tất cả các cạnh bằng a
 , điểm M thuộc cạnh SC sao cho SM= 2 MC . Mặt phẳng (P) chứa AM và song song BD. Tính diện 
 xa26 2 x
 tích của thiết diện của hình chóp S. ABCD bởi mặt phẳng (P) là S , với xy;,∈ là 
 ANMP y y
 phân số tối giản. Tính xy+ 
 Đáp số: 
 ax+1
Câu 45. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Biết rằng đồ thị hàm số y = có 
 bx − 2
 tiệm cận đứng là x = 2 và tiệm cận ngang là y = 3 . Tính ab+ . 
 Đáp số: 
Câu 46. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình lập phương ABCD. A′′′′ B C D
 có cạnh bằng a . Trên các cạnh BC và DD′ lần lượt lấy các điểm M và N sao cho 
 BM= DN = x (0 ≤≤xa) . 
 A D
 M
 B C
 N
 A' D'
 B' C'
 a
 Tính tỉ số để MN có độ dài nhỏ nhất. 
 x
 Đáp số: 
Câu 47. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Có bao nhiêu giá trị nguyên của tham số 
 3 22
 m để hàm số y=−++ x32( m) x 3( m + 4 mx) + 1 nghịch biến trên khoảng (0;1) ? 
 Đáp số: 
Câu 48. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho y= fx( ) là hàm số chẵn, có đạo 
 2 3 6
 hàm trên đoạn [−6;6]. Biết rằng ∫ fx( )d x= 8 và ∫ f(−=23 xx)d . Tính ∫ fx( )d x. 
 −1 1 −1
 Đáp số: 
 8 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
Câu 49. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình chóp S. ABCD có đáy ABCD 
 là hình bình hành. Từ một điểm M trên cạnh SA dựng đường thẳng song song với AD 
 SM CQ
 cắt SD tại điểm N . Trên cạnh CD lấy điểm Q sao cho = . 
 SA CD
 S
 M N
 B
 C
 Q
 A
 D 
 SA
 Điểm M trên SA sao cho diện tích của tam giác MNQ lớn nhất thì tỉ số bằng 
 SM
 Đáp số: 
Câu 50. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Có bao nhiêu giá trị nguyên thuộc 
 khoảng [0;5] của tham số m để bất phương trình 3logx≤ 2log ( mx − x2 −−(1 x) 1 − x) 
 có nghiệm thực ? 
 Đáp số: 
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 9 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 HƯỚNG DẪN 
 BẢNG ĐÁP ÁN 
 1.C 2.C 3.D 4.C 5.D 6.D 7.D 8.A 9.D 10.C 
 11.B 12.C 13.D 14.C 15.C 16.B 17.B 18.D 19.A 20.B 
 21.A 22.C 23.D 24.D 25.C 26.C 27.D 28.D 29.C 30.A 
 31.A 32.A 33.D 34.C 35.D 
 PHẦN ĐIỀN KHUYẾT 
Câu 36: Đáp số: 30 . 
Câu 37: Đáp số: 3. 
Câu 38: Đáp số: 3. 
Câu 39: Đáp số: 80. 
Câu 40: Đáp số: 1. 
Câu 41: Đáp số: 45. 
Câu 42: Đáp số: 4. 
Câu 43: Đáp số: 1. 
Câu 44: Đáp số: 17. 
Câu 45: Đáp số: 4. 
Câu 46: Đáp số: 2. 
Câu 47: Đáp số: 4. 
Câu 48: Đáp số: 14. 
Câu 49: Đáp số: 2. 
Câu 50: Đáp số: 3. 
 10 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
 LỜI GIẢI CHI TIẾT 
Câu 1. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Biểu đồ dưới đây mô tả số lượng tài khoản 
 chứng khoán mở mới theo tháng của nhà đầu tư trong nước (NĐT trong nước) và nhà đầu tư 
nước 
 ngoài (NĐTNN) vào Việt Nam 
 Khẳng định nào sau đây là khẳng định sai ? 
 A. Sau 6 tháng đầu năm 2021, nhà đầu tư trong nước đã mở mới 620.683 tài khoản chứng 
 khoán. 
 B. Trong tháng 6, nhà đầu tư nước ngoài đã mở mới 277 tài khoản chứng khoán. 
 C. Tháng 6/2021 nhà đầu tư trong nước mở hơn tháng 5/2021 là 140193 tài khoản chứng 
 khoán. 
 D. Tháng 6 nhà đầu tư nước ngoài mở thấp hơn 156 tài khoản so với tháng trước và là con 
 số thấp 
 nhất từ tháng 11/2020. 
 Lời giải 
 Chọn C 
Câu 2. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Nghiệm của phương trình 
 log3 ( 3x −= 1) 0 là 
 2 1
 A. x = 0 . B. x = 2 . C. x = . D. x = . 
 3 3
 Lời giải 
 Chọn C 
 1
 Điều kiện: 3xx−> 10 ⇔ > . 
 3
 2
 Ta có: log310( x−) = ⇔ 313 xx −=0 ⇔ = . 
 3 3
 2
 Vậy phương trình có nghiệm x = . 
 3
Câu 3. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Đường cong trong hình vẽ sau là đồ thị 
 của hàm số nào dưới đây? 
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 11 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 A. yx=−−3 21 x . B. yx=−−+3 21 x. C. y=−++ xx321. D. 
 yx=−+3 21 x . 
 Lời giải 
 Đồ thị hàm số có nhánh ngoài cùng bên phải hướng lên nên loại B và C. 
 Ta có: y (00) > nên loại A. 
 x +1
Câu 4. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Tiệm cận ngang của đồ thị hàm số y = là 
 x −1
 A. y = 2 . B. y = 0. C. y =1. D. y = −1. 
 Lời giải 
 Chọn C 
 x +1
 Ta có lim= 1nên đồ thị hàm số có tiệm cận ngang y =1. 
 x→±∞ x −1
Câu 5. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình nón có bán kính đáy r = 3 
 và độ dài đường sinh l = 4. Diện tích xung quanh của hình nón đã cho là 
 A. Sxq = 39π . B. Sxq =12π . C. Sxq = 83π . D. Sxq = 43π . 
 Lời giải 
 Chọn D 
 Diện tích xung quanh của hình nón là Sxq =ππ rl = 43. 
Câu 6. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số fx( ) có đạo hàm trên . 
 fx( )
 Biết Fx( ) = sin x là một nguyên hàm của trên khoảng (0; +∞), họ tất cả các nguyên 
 x
 hàm của hàm số gx( ) = f′( x)ln x là 
 A. xln x sin x++ cos xC. B. xln x sin x−+ cos xC. 
 C. xln x cos x++ sin xC. D. xln x cos x−+ sin xC. 
 Lời giải 
 Chọn D 
  1
 ux= ln ddux=
 Đặt ⇒ x . 
 ddv= fxx′( ) 
 v= fx( )
 fx( )
 Khi đó fxxxfxx′( )ln d=( ) ln − d xfxx =( ) ln −+ sin xC. 
 ∫∫x
 12 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
 fx( )
 Mặt khác, do sin x là một nguyên hàm của trên khoảng (0; +∞) nên 
 x
 fx( ) fx( )
 (sin x)′ = hay cos x= ⇔= fx( ) xcos x. 
 x x
 Vậy ∫ f′( x)ln xx d= x ln x cos x −+ sin x C. 
 2
Câu 7. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Bất phương trình 4.2xx−< 2 0 có 
 nghiệm là 
 A. x ∈( −∞;2) . B. x ∈( −∞; − 1) ∪( 2; +∞) . 
 C. x ∈( −1; +∞) . D. x ∈−( 1; 2) . 
 Lời giải 
 Chọn D 
 2 2
 Ta có 4.2xx−< 2 0 ⇔<22xx+2 ⇔+<xx2 2 ⇔−xx2 + +20 < ⇔−12 <x < . 
Câu 8. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trong không gian với hệ tọa độ Oxyz , 
 mặt phẳng (P) đi qua M (−−1;3; 2) nhận véctơ n =(3;4; − 2) làm véctơ pháp tuyến. Mặt 
 phẳng (P) có phương trình là: 
 A. 3xyz+ 4 −−= 2 13 0 . B. 3xyz+ 4 −+= 2 19 0 . 
 C. −+xyz3 − 2 + 40 = . D. −+3xyz 4 − 2 −= 13 0 . 
 Lời giải 
 Chọn A 
 MP(−1;3; −∈ 2) ( )
 Mặt phẳng (P) :  có phương trình là: 
  vtpt: n =( 3;4; − 2)
 3( xyz++ 14) ( −− 32) ( + 2) = 0 
 ⇔3xyz + 4 − 2 +− 3 12 − 4 
 ⇔3xyz + 4 −−= 2 13 0 . 
 Vậy mặt phẳng (P) có phương trình là (Pxyz) :3+ 4 −−= 2 13 0. 
Câu 9. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho các số thực ab,0≠ thoả mãn 
 a
 34ab= . Giá trị của bằng 
 b
 A. log4 3 . B. ln12. C. ln 0,75 . D. log3 4 . 
 Lời giải 
 Chọn D 
 a ln 4
 Ta có: 3ab= 4 ⇒ab .ln 3 = .ln 4 ⇒= =log 4 . 
 b ln 3 3
Câu 10. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trên mặt phẳng tọa độ Oxy , tập hợp tất 
 cả điểm biểu diễn của số phức z thỏa mãn 35+−i zi = là đường tròn có phương trình 
 22 22
 A. ( xy−1) ++( 35) =. B. ( xy+1) +−( 3) = 25 . 
 22 22
 C. ( xy−1) ++( 3) = 25 . D. ( xy+1) +−( 35) =. 
 Lời giải 
 Chọn C 
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 13 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 Gọi z=+∈ x yi ( x, y ) . 
 Ta có: 35+−i zi = . 
 ⇔3 +−i( x + yi) i = 53 ⇔( +y) +( 1 − x) i = 5 
 22 2 2
 ⇔(3 +yx) +−( 1) =⇔ 5( xy − 1) +( + 3) = 25 . 
Câu 11. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Tìm giá trị nhỏ nhất của hàm số 
 fx()= x2 − 3 x −− 4 xtrên đoạn [−2;6] 
 A. 1. B. 4. C. 0 . D. 5 . 
 Lời giải 
 Chọn B 
 Nếu x ∈−[ 1; 4 ] thì fx()=−+ x2 2 x + 4. 
 Khi đó fx'()=−+⇒ 2 x 2 fx '()0 =⇔= x 1. 
 Ta có f(−= 1) 1; ff (1) = 5; (4) =− 4 . 
 Nếu x ∈−[ 2; − 1] ∪[ 4;6] thì fx()=−− x2 4 x 4. 
 Khi đó fx'( )= 2 x −⇒ 4 fx '( ) =⇔ 0 x = 2 . 
 Ta có f(−= 2) 8; f ( −= 1) 1; ff (6) = 8; (4) =− 4 . 
 So sánh hai trường hợp minfx ( )= f (4) = − 4 . 
 [−2;6]
Câu 12. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Có bao nhiêu giá trị nguyên của tham số
 x −1
 m∈−[ 10;10] sao cho đồ thị hàm số y = có hai đường tiệm cận đứng? 
 26x2 + xm −− 3
 A. 19. B. 15. C. 17 . D. 18. 
 Lời giải 
 Chọn C 
 x −1
 Ta có đồ thị hàm số y = có hai đường tiệm cận đứng khi phương trình 
 26x2 + xm −− 3
 322 −( −−m 30) >
 2x2 + 6 xm − −= 30 có hai nghiệm phân biệt khác 1 ⇔ 
  2
 2.1+ 6.1 −m −≠ 3 0
  15
 m >−
 ⇔  2 
 m ≠ 5
 Từ đó ta suy ra tập các giá trị nguyên của m thỏa mãn là 
 {−−−−−−−7, 6, 5, 4, 3, 2, 1,0,1,2,3, 4,6,7,8,9,10} . Vậy có 17 giá trị nguyên của m thỏa 
 mãn. 
Câu 13. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trong không gian Oxyz, cho mặt cầu 
 (S ) nhận AB là đường kính biết tọa độ A(3; 2;1) ; B(−1; 4; 3 ) . Phương trình mặt cầu (S ) 
 là 
 222 222
 A. ( xyz+1) ++( 3) ++( 2) = 24. B. ( xyz+1) ++( 3) ++( 2) = 6. 
 222 222
 C. ( xyz−1) +−( 3) +−( 2) = 24. D. ( xyz−1) +−( 3) +−( 2) = 6. 
 Lời giải 
 Chọn D 
 14 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
 x+++ xy yz z
 Tọa độ trung điểm I của AB là IIA B;; A BA B⇒ (1; 3; 2 ) . 
 222
 2 22
 IA =(13 −) +−( 32) +−( 21) = 6. 
 Vì mặt cầu (S ) nhận AB là đường kính suy ra mặt cầu (S ) nhận I (1; 3; 2 ) là tâm và bán 
 kính R= IA = 6 . 
 22
 Phương trình mặt cầu là: ( xyz−1) +( − 3) +− ( 2)2 = 6. 
 2 3
Câu 14. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Nếu ∫ ft( )d4 t= − và ∫ fu( )d5 u= thì 
 1 2
 3
 ∫ fx( )d x bằng: 
 1
 A. −9 . B. −1. C. 1. D. 9. 
 Lời giải 
 Chọn C 
 32323
 Ta có ∫∫∫∫∫fx( )d x= fx( ) d x + fx( ) d x = ft( ) d t + fu( ) d u =−+= 451. 
 1 1 2 12
Câu 15. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Hàm số nào dưới đây đồng biến trên tập 
 xác định của nó. 
 x x x
 e 1 x 1
 A. y = . B. y = . C. y = ( π ) . D. y = . 
 π π e
 Lời giải 
 Chọn C 
 x
 Ta có hàm số y = ( π ) có cơ số π >1. Nên hàm số đồng biến trên TXĐ của nó. 
Câu 16. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Họ tất cả các nguyên hàm của hàm số 
 fx( ) =2 x + sin x là 
 2 2
 A. x++cos xC. B. x−+cos xC. 
 2 ++ 2 −+
 C. 2x cos xC. D. 2x cos xC. 
 Lời giải 
 Chọn B 
 ∫∫fx( ) =+(2 x sin xx) d =−+ x2 cos xC. 
Câu 17. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình trụ biết rằng khi cắt hình trụ 
 đã cho bởi một mặt phẳng qua trục, thiết diện thu được là một hình vuông và có diện tích 
 bằng 32. Diện tích xung quanh của hình trụ đã cho bằng: 
 A. 16π . B. 32π . C. 64π . D. 48π . 
 Lời giải 
 Chọn B 
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 15 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 Giả sử thiết diện của hình trụ là hình vuông ABCD . 
 Theo đầu bài ta có SABCD =⇒==32 AB BC 4 2 . 
 AB
 Từ đó suy ra r = =22,l = BC = 42. 
 2
 Vậy diện tích xung quanh của hình trụ là Sxq =2ππ rl = 2. .2 2.4 2= 32 π. 
Câu 18. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho đa giác đều có 2022 đỉnh. Số hình 
 chữ nhật có 4 đỉnh là 4 trong số 2022 điểm là đỉnh của đa giác đã cho là 
 4 4 2 2
 A. C2022 . B. C1011 . C. C2021 . D. C1011 . 
 Lời giải 
 Chọn D 
 Đa giác đều có 2022 đỉnh thì có 1011 đường chéo đi qua tâm. 
 Cứ 2 đường chéo đi qua tâm tạo được 1 hình chữ nhật. 
 2
 Vậy số hình chữ nhật là C1011 . 
Câu 19. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Bác An xây bể hình trụ có thể tích 150m3
 . Đáy bể làm bằng bê tông giá 100000 đồng /m2 . Phần thân làm bằng tôn giá 90000 đồng
 /m2 , nắp bằng nhôm giá 120000 đồng /m2 . Hỏi để chi phí sản xuất bể đạt mức thấp nhất 
 thì tỷ số giữa chiều cao bể và bán kính đáy là bao nhiêu? 
 22 9 31 22
 A. . B. . C. . D. . 
 9 22 22 31
 Lời giải 
 Chọn A 
 150
 Gọi rh, lần lượt là bán kính đáy và chiều cao bể trụ. Ta có V=π rh2 =150 ⇒= h . 
 π r 2
 Chi phí làm bể trụ là 
 T=+100000π r 2 2.90000 ππrh +=+ 120000 r 22 220000 ππr 180000 rh 
 2 27000000
 ⇒=Tr220000π + 
 r
 27000000 440000π r3 − 27000000
 ⇒=Tr′ 440000π − = 
 rr22
 3 675
 ⇒Tr′ =⇒0 440000π − 27000000 =⇒= 0 r3 
 11π
 675
 r 0 11π +∞
 T' 0 +
 T
 16 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
 675h 150 22
 Suy ra T đạt giá trị nhỏ nhất khi r =3 ⇒= = . 
 11ππrr3 9
Câu 20. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Nghiệm của phương trình 
 log4 (x −= 1) 2 là 
 9 7
 A. x = 3. B. x =17 . C. x = . D. x = . 
 2 2
 Lời giải 
 Chọn B 
 Điều kiện xx−>10 ⇔ > 1. 
 Phương trình log4 (xxx− 1) = 2 ⇔ −= 1 16 ⇔ = 17 (nhận) 
 Vậy nghiệm của phương trình x =17 . 
Câu 21. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Một hộp bóng bàn có dạng hình hộp chữ 
 nhật. Biết rằng hộp chứa vừa khít ba quả bóng bàn được xếp theo chiều dọc, các quả bóng 
 bàn có kích thước như nhau. 
 Phần không gian còn trống trong hộp chiếm tỉ lệ 
 A. 47,% 64 . B. 65,% 09 . C. 82,% 55 . D. 83,3% . 
 Lời giải 
 Chọn D 
 Giả sử bán kính của mỗi quả bóng bàn là r thì khi đó hộp đựng bóng bàn sẽ có kích thước 
 4
 là 226rrr××. Khi đó tổng thể tích của ba quả bóng bàn sẽ là 3. .π=π .r33 4 r . 
 3
 Thể tích của hộp sẽ là 2rrr .2 .6= 24 r3 . Vậy phần không gian còn trống trong hộp sẽ là: 
 (24− 4π )r3
 Vr=2433 − 4π r sẽ chiếm .100%≈ 47,64% . 
 1 24π r3
 2*
Câu 22. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho dãy số (un ) , biết unn =+∈1, n 
 . Số 7922 là số hạng bao nhiêu trong dãy? 
 A. 79 . B. 69 . C. 89 . D. 99 
 Lời giải 
 Chọn C 
 =
 2 n 89
 Ta có un = 7922 ⇔n +=1 7922 ⇔  . 
 n = −89
 Vì n∈ ∗ nên n = 89 . 
Câu 23. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trong không gian với hệ tọa độ Oxyz , 
 cho ba điểm M (3;0;0) , N (0;− 2;0) và P(0;0; 2) . Mặt phẳng (MNP) có phương trình là 
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 17 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 xyz xyz xy z xyz
 A. + +=−1. B. + +=0 . C. ++ =1. D. + +=1
 3− 22 3− 22 32− 2 3− 22
 . 
 Lời giải 
 Chọn D 
 xyz
 Theo phương trình đoạn chắn, mặt phẳng (MNP) có phương trình là + +=1. 
 3− 22
Câu 24. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hình trụ có bán kính đáy r , gọi O
 và O ' là tâm của hai đường tròn đáy với OO′ = 2 r . 
 Một mặt cầu tiếp xúc với hai đáy của hình trụ tại O và O ' . Gọi VC và VT lần lượt là thể 
 VC
 tích của khối cầu và khối trụ. Khi đó bằng 
 VT
 3 3 1 2
 A. . B. . C. . D. . 
 5 4 2 3
 Lời giải 
 Chọn D 
 4
 π r3
 V 2
 C =3 =
 Ta có 2 . 
 VT π rr2 3
Câu 25. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Trong không gian Oxyz, cho điểm 
 xy−−12 z
 A(2;2;1) và đường thẳng d : = = ; 
 1 21 2
 xyz−−32
 d : = = . Phương trình đường thẳng d đi qua A, vuông góc với d và cắt d 
 2 1 23 1 2
 là 
 xyz−−−2 21 x−−12 yz
 A. d : = = . B. d : = = . 
 1−− 35 23− 4
 xt=2 +
  xyz−−−2 21
 C. dy:2 =( t ∈ ) . D. d : = = . 
  −−12 3
  zt=1 −
 Lời giải 
 Chọn C 
 18 CHINH PHỤC MỌI MIỀN KIẾN THỨC 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC 2022-TEAM EMPIRE 
 d2
 B
 A
 d1
   
 Vectơ chỉ phương của d , d lần lượt là u = 2;1; 2 , u = 1; 2; 3 . 
 1 2 d1 () d2 ()
  
 Giả sử d∩ d22 =⇒∈ B Bd. Gọi B(3++ t ;22;3t t)( ⇒ AB 1 + t ;2;3 t t − 1) . 
   
 Vì d⊥ d1 ⇒ AB ⊥ udd11 ⇔ AB. u = 0 ⇔ 21()() +t + 2 t + 23 t − 1 = 0 ⇔= t 0. 
  
 Khi đó AB()1; 0;− 1 . 
 xt=2 +
  
 d đi qua A()2 ;1 ;2 và có VTCP là AB()1; 0;− 1 , nên có phương trình :  yt=2 () ∈ 
 
  zt=1 −
 . 
 xy+=4
Câu 26. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hệ phương trình  22 2. 
 xym+=
 Khẳng định nào sau đây là đúng? 
 A. Hệ phương trình luôn vô nghiệm. 
 B. Hệ phương trình có nghiệm với mọi m . 
 C. Hệ phương trình có nghiệm ⇔≥m 8 . 
 D. Hệ phương trình có nghiệm duy nhất ⇔≥m 2. 
 Lời giải 
 Chọn C 
 xy+=4 16 − m2
 ⇒ 22−=⇒=
 Ta có :  22 2 24 Pm P 
 xym+= 2
 ⇒S2 − 4P = 16−− 2()16− mm22= 216 ≥ 0 ⇔≥m 8 . 
Câu 27. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Theo hình thức lãi kép, một người vay 
 ngân hàng số tiền 500 triệu đồng, lãi suất theo kì hạn 1 tháng là 1%. Người này trả nợ đều 
 đặn cho ngân hàng mỗi tháng cùng một số tiền là 10 triệu đồng. Hỏi sau ít nhất bao nhiêu 
 tháng thì người này trả hết nợ bao gồm cả gốc lẫn lãi? 
 A. 68 (tháng). B. 72 (tháng). C. 69 (tháng). D. 70 (tháng). 
 Lời giải 
 Chọn D 
 Số tiền còn phải trả sau tháng thứ nhất là A1 =+−500(1 0,01) 10. 
 Số tiền còn phải trả sau tháng thứ hai là 
 2
 AA21=(1 + 0,01) −= 10 500(1 + 0,01) −− 10 10(1 + 0,01). 
 Số tiền còn phải trả sau tháng thứ n là 
 (1+− 0, 01)n 1
 A =500(1 + 0,01)n −++ 10 10(1 0,01) +++ ... 10(1 0,01)nn−1 = 500(1 + 0,01) − 10 . 
 n 0,01
 CHINH PHỤC MỌI MIỀN KIẾN THỨC 19 
 LUYỆN THI ĐÁNH GIÁ NĂNG LỰC HCM 2022-TEAM EMPIRE 
 Sau tháng thứ n hết nợ nên An = 0, vì vậy 
 (1+− 0,01)nn 1 (1 +− 0,01) 1 500 × 0,01
 500(1+− 0,01)n 10 =⇔0 =
 0,01 (1+ 0,01)n 10
 11
 ⇔−1 = ⇔(1 + 0,01)n = 2 ⇔n = log 2 ≈ 69,66.
 (1+ 0, 01)n 2 1,01
 Vậy sau ít nhất 70 tháng thì người đó trả hết nợ cho ngân hàng. 
Câu 28. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số y= fx() xác định và liên 
 tục trên []−1; 5 có đồ thị của hàm số y= fx′() được cho như hình vẽ. Hàm số 
 gx() = f() x2 −−21 x đồng biến trên khoảng nào dưới đây? 
 A. ()−∞;1 . B. ()1;+∞ . C. ()0; 2 . D. ()−1; 0 . 
 Lời giải 
 Chọn D 
 Ta có gx′′()()=2 x − 2. f() x2 −− 2 x 1 
 2 22x <−1
 Ta có: fxx′()−−210>⇔−−>⇔−−>⇔ xx 212 xx 230  
  x > 3
 xx=10=
 ′ 2
 gx() =0 ⇔ x − 21 x −=−⇔ 1x =± 1 
 2
 xx−2 −= 1 2 x =− 1; x = 3
 Ta có BBT 
 Dựa vào BBT ta thấy hàm số đồng biến trên ()−1; 0 . 
Câu 29. [LUYỆN THI ĐGNL 2022 - TEAM EMPIRE] Cho hàm số y=+() m23 x32 + x +− mx 5
 , m là tham số. Tìm các giá trị của m để các điểm cực đại, cực tiểu của đồ thị hàm số đã 
 cho có hoành độ là các số dương. 
 20 CHINH PHỤC MỌI MIỀN KIẾN THỨC